e100
0 1 2 7
58 34 7 1 Statistical Modeling
Advanced Statistics and Data Analysis
What is statistics
What is statistics
Statistics is the art of making numerical conjectures about puzzling questions.
Freedman et al., 1978.
The objective of statistics is to make inferences (predictions, decisions) about a population based on information contained in a sample.
Mendenhall, 1987.
What are statistical models
Statistical models are sets of equations involving random variables
Statistical models involve distributional assumptions
Given a question and a body of data statistical models can be used to provide answers along with measures of uncertainty.
What are statistical models
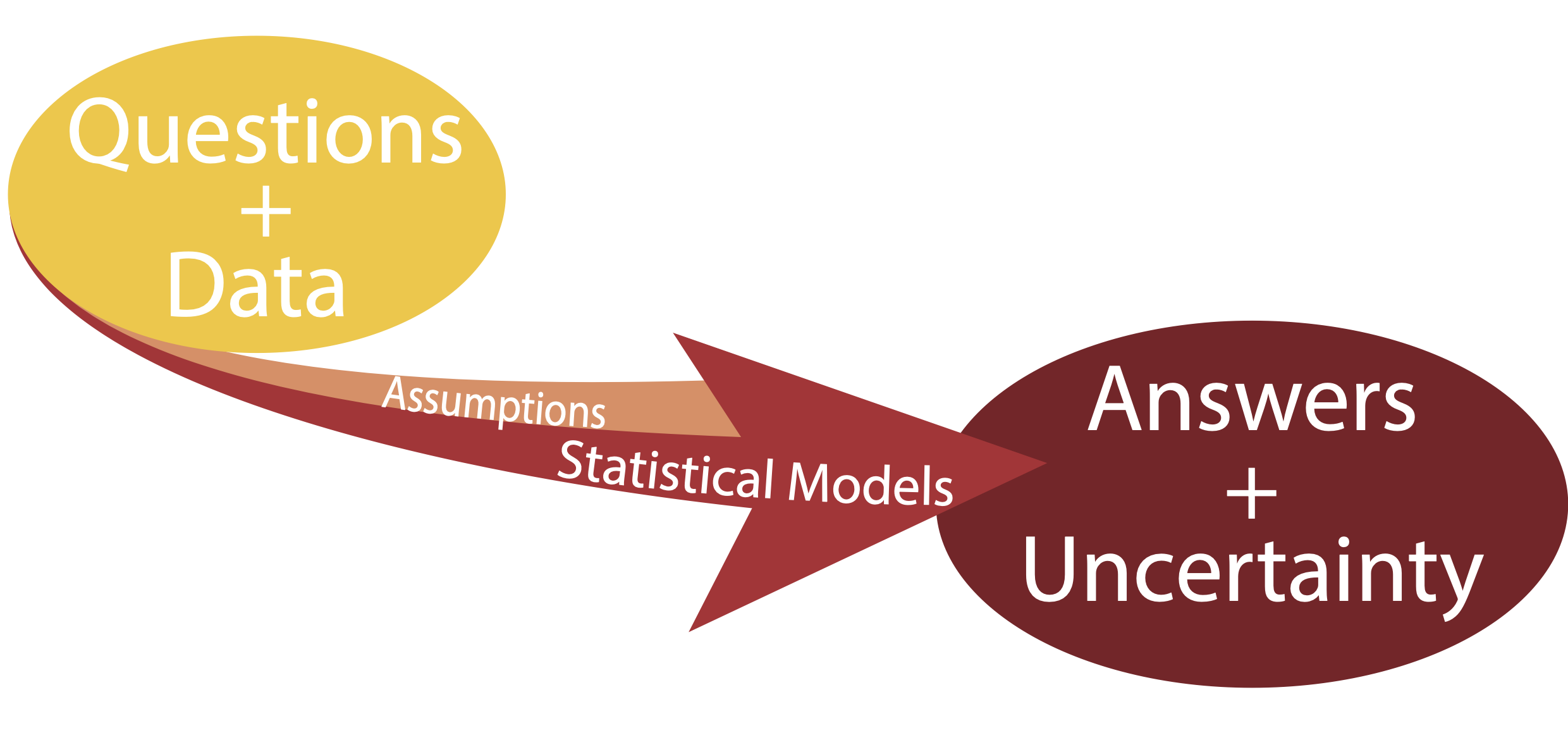
Statistical Models
Three key concepts: question, model, uncertainty
Far better an approximate answer to the right question, which is often vague, than an exact answer to the wrong question, which can always be made precise.
John W. Tukey, 1962.
All models are wrong, but some are useful.
George E. P. Box, 1987.
Statistical Inference
Statistical Inference
Statistical inference is the process of learning some properties of the population starting from a sample drawn from this population.
For instance, we may be interested in learning about the survival outcome of cancer patients, but we cannot measure the whole population.
We can however measure the survival of a random sample of the population and then infer or generalize the results to the entire population.
Statistical Inference
There are some terms that we need to define.
- The data generating distribution is the unknown probability distribution that generates the data.
- The empirical distribution is the observable distribution of the data in the sample.
We are usually interested in a function of the data generating distribution. This is often referred to as parameter (or the parameter of interest).
We use the sample to estimate the parameter of interest, using a function of the empirical distribution, referred to as estimator.
Statistical Inference
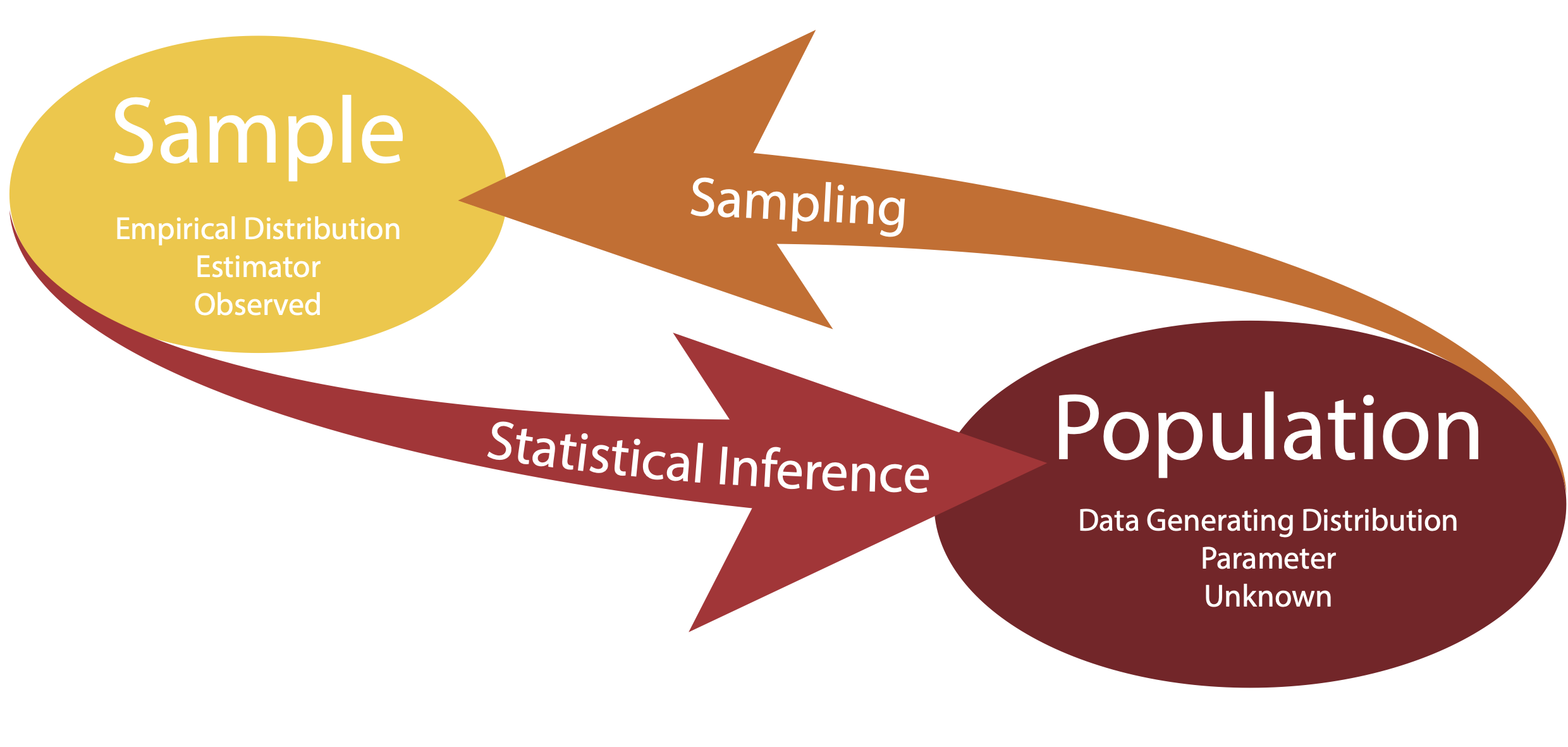
Statistical Inference
Statistical Inference
Parameter: unknown object of interest.
Estimator: data-driven guess at the value of the parameter.
In terms of mathematical notation, we often use Greek letters to refer to parameters and we use the same letter with the “hat” notation to refer to their estimate.
For instance, we denote with \(\hat{\theta}\) the estimator of the parameter \(\theta\).
Sometimes, you will find the notation \(\hat{\theta}_n\), when we want to emphasize that we are using a sample of \(n\) observations to estimate the parameter.
Example: Blood pressure in healthy individuals
Let’s assume that we want to estimate the average blood pressure of healthy individuals in the United States.
Let’s assume that we have access to blood pressure measurements for a random sample of the population (more on this later!).
- What is the parameter of interest?
- How can we estimate the parameter using the data in our sample?
Data generating distribution
The data generating distribution is unknown.
In nonparametric statistics we aim at estimating this distribution from the empirical distribution of the sample, without making any assumptions on the shape of the distribution.
However, it is often easier to make some assumptions about the data generating distribution. These assumptions are sometimes based on domain knowledge or on mathematical convenience.
One commonly used strategy is to assume a family of distributions for the data generating distribution, for instance the Gaussian distribution.
Probability
Probability
In order to make inference from a random sample to the whole population, we need some notion of randomness. To study randomness we need the concept of probability.
Hence, probability is one of the foundation of statistical inference.
However, probability is only a tool and statistics deals with how to model observed data using a probabilistic model.
What is a probability measure?
Answering this question properly would require a semester-long course.
However, for our purpose, we are only interested in probability as a measure that quantifies the randomness of an event. E.g., the probability of obtaining “heads” when tossing a coin.
Remember that:
- The probability of an event is a number between 0 and 1.
- The sum of the probabilities of all possible events is 1.
- The probability of the union of two disjoint events is the sum of their probabilities.
Central concept
The central concept in probability is the probability space, which is assumed to have three components.
A sample space \(S\), i.e., a universe of “possible” outcomes for the experiment in question.
A designated collection of “observable” subsets, called events, of the sample space.
A probability measure, a function that assigns real numbers, called probabilities, to events.
Example
A fair coin is tossed twice. What is the probability of observing exactly one Head?
The sample space is \(S=\{HH,HT,TH,TT\}.\) Because the coin is fair, each of the four outcomes in \(S\) is equally likely.
Let \(A\) denote the event that exactly one Head is observed. Then, \(A = \{HT, TH\},\) and \[P(A) = \frac{\#(A)}{\#(S)} = \frac{2}{4} = 0.5.\]
Conditional Probability
A fair coin is tossed twice. Suppose that we toss the coins once and we observe Tail. What is now the probability of observing exactly one Head?
We denote with \(B\) the event that we observed (that the first toss is Tail), and with \(A\) the event that exactly one Head is observed.
As before, \(A = \{HT, TH\}\), but we have \(B = \{TH, TT\},\) so the only event in \(A\) that is compatible with \(B\) is \(\{TH\}\).
We hence computed the conditional probability of the event \[ P(A | B) = \frac{\#(A \cap B)}{\#(S \cap B)} = \frac{1}{2} = 0.5. \]
What would be the conditional probability if the first coin was Head?
Conditional Probability
If \(A\) and \(B\) are events, and \(P(B) > 0\), the conditional probability of \(A\) given \(B\) is \[P(A|B) = \frac{P(A\cap B)}{P(B)} .\]
The same equality can be written as: \[P(A|B) P(B)= P(A\cap B).\]
Example: COVID-19 test
Thanks to Laura Ventura
Suppose that we perform a test to check whether we have contracted COVID-19. The possible observable outcomes are two: we have contracted the virus \((D),\) or we have not \((H)\).
From the latest statistical analyses, we can estimate the prevalence of the disease in the population, \(P(D)\), i.e., the probability that an individual selected at random from the population is infected.
Diagnostic Test
A test is designed to detect the presence of the SARS-CoV-2 virus in the nose and throat. This test also has two possible outcomes: positive for the presence of viral RNA \((+),\) negative for the presence of viral RNA \((-)\).
Because diagnostic procedures undergo extensive evaluation before they are approved for general use, we have a fairly precise notion of the probabilities of a false positive, i.e., the probability of obtaining a positive test result given that the patient is not infected, and a false negative, i.e., the probability of obtaining a negative test results given that the patient is infected.
These probabilities are conditional probabilities: the probability of a false positive is \(P(+|H),\) and the probability of a false negative is \(P(-|D)\).
Predictive Value of the Test
The gold standard test for COVID-19 has a false positive and false negative rate of about \(5\%\).
Assume that there is a COVID-19 prevalence of about \(8\%\) in the Italian population.
Assume \(P(D) = .08,\) \(P(+|H) = .05\) and \(P(-|D) = .05\).
(This implies \(P(H) = .92,\) \(P(-|H) = .95\) and \(P(+|D) = .95\).)
What is the predictive value of the test, i.e., the probability that we don’t have COVID-19 if the test is negative?
The question asks to compute the quantity \(P(H|-).\) By definition, we have \[P(H|-) = \frac{P(H\cap -)}{P(-)} = \frac{P(-|H) P(H)}{P(-)}.\]
Computations
We know that \[P(H \cap -) = P(H) P(-|H) = 0.92 \times 0.95,\]
\[P(D \cap -) = P(D) P(-|D) = 0.08 \times 0.05,\]
\[P(H \cap +) = P(H) P(+|H) = 0.92 \times 0.05,\]
\[P(H \cap -) = P(H) P(-|H) = 0.92 \times 0.95,\]
\[P(-) = P(D \cap -) + P(H \cap -)=0.08 \times 0.05 + 0.92 \times 0.95.\]
Therefore, \[P(H|-) = \frac{P(H\cap -)}{P(-)} = \frac{0.92 \times 0.95}{0.08 \times 0.05 + 0.92 \times 0.95}=0.995.\]
Bayes’ Theorem
Note that we have just used one of the most important theorems in modern statistics, Bayes’ Theorem.
The theorem states: \[ P(B | A) = \frac{P(A | B) P(B)}{P(A)}. \]
In words, if we know the conditional probability of \(A\) given \(B\), in addition to the marginal probabilities of the two events, we have a rule to compute the conditional probability of \(B\) given \(A\).
Independence
Two events are independent if the occurrence of either is unaffected by the occurrence of the other.
Let \(A\) and \(B\) denote events and assume for the moment that the probability of each is strictly positive.
If \(A\) and \(B\) are to be regarded as independent, then the occurrence of \(A\) is not affected by the occurrence of \(B\).
This can be expressed by writing \[P(A|B) = P(A),\]
or, equivalently, \[P(A \cap B) = P(A)P(B).\]
Random Variables
Informally, a random variable is a rule for assigning real numbers to experimental outcomes.
By convention, random variables are usually denoted by upper case Roman letters near the end of the alphabet, e.g., \(X\), \(Y\), \(Z\).
Examples
Example 1. A coin is tossed once and the occurrence of Head is recorded.
We have: \(S=\{H,T\}\). It is convenient to assign the real number 1 to outcome Head, and the real number 0 to the other outcome, Tail.
A random variable \(X\) for this experiment can be defined as the function \(X: S \longrightarrow R\) such that: \[X(H) = 1,\] \[X(T) = 0.\]
Examples
Example 2. A coin is tossed twice and the number of Heads is recorded.
We have: \(S=\{HH,HT,TH,TT\}\). It is often convenient to assign the real number 1 to one outcome, Head say, and the real number 0 to the other, Tail.
A random variable \(X\) for this experiment can be defined as the function \(X: S \longrightarrow R\) such that: \[X(HH) = 2,\] \[X(HT) = X(TH) = 1,\] \[X(TT) = 0.\]
Random Variables
A variable is a measurement that describe a characteristic of a set of observations.
A random variable (r.v.) is a variable that measures an intrinsically random process, e.g. a coin toss.
Before observing the outcome, we will not know with certainty whether the toss will yield “heads” or “tails”, but that does not mean that we do not know anything about the process: we know that on average it will be heads half of the times and tails the other half.
If we refer to \(X\) as the process of measuring the outcome of a coin toss, we say that \(X\) is a random variable.
Statistical inference
It is somewhat confusing to talk about random variables in the context of statistical inference.
For instance, let’s say that we want to describe the height of a certain population. The height of an individual is not a random quantity! We can measure with a certain amount of precision the height of any individual.
What is random is the process of sampling a set of individuals from the population.
In other words, the randomness comes from the sampling mechanism, not from the quantity that we are measuring: if we repeat the experiment, we will select a different sample and we will obtain a different set of measurements.
Rationale
The primary reason that we construct a random variable, \(X\), is to replace the probability space that is naturally suggested by the experiment in question with a familiar probability space in which the possible outcomes are real numbers.
Thus, we replace the original sample space, \(S\), with the familiar real line, \(\mathbb{R}\).
To complete the transfer, we must decide which subsets of \(\mathbb{R}\) will be designated as events and we must specify how the probabilities of these events are to be calculated.
Statistical modeling
The art of statistical modeling
Start with the data: exploratory data analysis (EDA).
Make probabilistic assumptions: choose a distribution.
Make inference: estimate the parameters of the distribution.
A simple example
When testing certain pharmaceutical compounds, it is important to detect proteins that provoke an allergic reaction.
The molecular sites that are responsible for such reactions are called epitopes.
ELISA assays are used to detect specific epitopes at different positions along a protein.
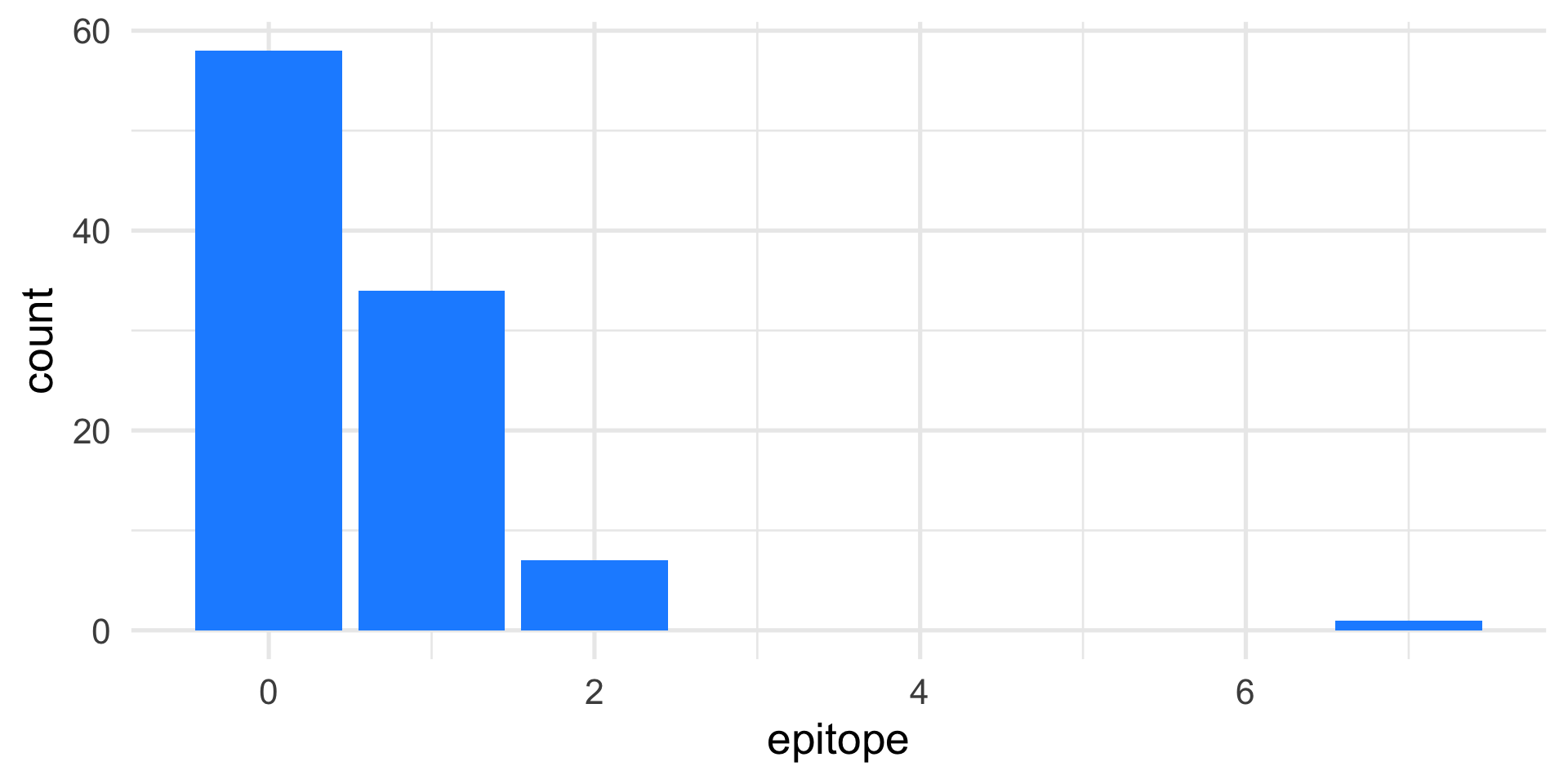
The protein is tested at 100 different positions, supposed to be independent.
We collect data from 50 patients, the reactions are summed at each location.
Start with the data: EDA
Make probabilistic assumptions
The Poisson distribution is a good model for counting rare events.
Would its distribution look similar to the one we observe?
First, we need to recall that the Poisson distribution depends on one parameter, namely \(\lambda\), which is also the mean (or expected value) of the distribution.
We can visually compare the observed distribution with a Poisson, with different values of \(\lambda\).
Check the goodness of fit
Observed data:
Check the goodness of fit
It seems that the simulated data have higher counts than our observed data.
We could try \(\lambda = 2\):
We could continue with all possible values of \(\lambda\) and choose the one that minimizes the differences between the observed and simulated data.
Compute the likelihood function
In other words, we want to compute the likelihood that the data come from the Poisson distribution with a given value of \(\lambda\), for any given value.
Since \(\lambda \in \mathbb{R}_+\), it is infeasible to try all possible values, and we can use a more elegant approach that uses the known form of the Poisson distribution to compute it.
Compute the likelihood function
What we want to compute is the probability that a Poisson r.v. with parameter \(\lambda\) will take the observed values. In R:
The function that we just computed is called the likelihood function and can be written as \[ L(\lambda, x) = \prod_{i=1}^n p(x_i), \] where \(p(x_i)\) is the probability mass function of a Poisson r.v.
Compute the log-likelihood function
For computational reasons, it is convenient to work with the log-likelihood, which sums the log of the pdf, and is usually indicated with the lowercase \(\ell\).
\[ \ell(\lambda, x) = \sum_{i=1}^n \log p(x_i). \]
Search for the best \(\lambda\)
# Define a grid of lambdas
lambdas = seq(0.05, 0.95, length = 100)
# Compute the log-likelihood
loglikelihood = vapply(lambdas, loglik, numeric(1))
# Find the value that maximizes the log-likelihood
lambda_hat <- lambdas[which.max(loglikelihood)]
df <- data.frame(lambdas, loglikelihood)
p1 <- ggplot(df, aes(lambdas, loglikelihood)) +
geom_line() +
geom_vline(xintercept = lambda_hat, col = "red") +
geom_hline(yintercept = max(loglikelihood), col="blue")
lambda_hat[1] 0.55Search for the best \(\lambda\)

Classical statistics
What we have just done is to find a value of the parameter that maximizes the log-likelihood function.
Maths tells us that to find the maximum (or minimum) of a function we can compute its derivative.
In this case, the log-likelihood function is easy to compute from the Poisson pdf: \[ p(x) = \frac{1}{x!}\lambda^x e^{-\lambda}. \]
Hence \[ \ell(\lambda, x) = \sum_{i=1}^n -\lambda + x_i \log \lambda - \log(x!) \]
Classical statistics
We obtain \[ \ell(\lambda, x) = -n \lambda + \log \lambda \sum_{i=1}^n x_i - c, \]
from which we can derive \[ \frac{d \ell}{d\lambda} = -n + \frac{1}{\lambda} \sum_{i=1}^n x_i, \]
that leads to \[ \hat{\lambda} = \frac{1}{n} \sum_{i=1}^n x_i. \]
Hence, the sample mean.
Maximum Likelihood Estimation
We have just seen one of the most important procedures of statistical inference: Maximum Likelihood Estimation.
We call \(\hat{\lambda}\) the maximum likelihood estimate (MLE).
In the case of the Poisson distribution, the MLE is the mean of the sample.
Maximum Likelihood Estimation is a staple of modern statistics. We will see that in more complex models, we do not have a closed form solution for it and we will need to rely on numerical algorithms.
Another example
Suppose that we take a sample of \(n = 120\) males and test them for color blindness.
We can code with \(x_i=0\) if subject \(i\) is not colorblind, and with \(x_i = 1\) if subject \(i\) is colorblind.
Suppose that we obtain the data summarized in the following table.
cb
0 1
110 10 Another example
- Assume that the data arise from a binomial r.v. with \(n=120\) trials and unknown success probability \(p\).
- What is your best guess at the value of \(p\)? Why?
- Use the
dbinomfunction in R to compute the likelihood for a grid of values of \(p\) and determine numerically the MLE. - Plot the log-likelihood function.
- Recall that the binomial pdf is \[ p(x) = \binom{n}{x} p^x (1-p)^{(n-x)} \]
- Use the derivative of the log-likelihood to compute the MLE.
To sum up
A statistical model uses probability distributions and random variables to provide a generative mechanism for the data that we observe.
Random variables are used to account for the statistical randomness that we have in our observed samples.
It is important to think carefully about what assumptions we are relying on when specifying a statistical model.
To sum up
The Maximum Likelihood Estimate (MLE) is the value of the parameter that maximizes the likelihood that the data arise from that distribution.
We obtain the MLE by maximizing the log-likelihood.
In simple models, we can use the derivative of the log-likelihood to obtain a closed-form estimate of the parameter.
In more complex models, we need to rely on numerical methods to maximize the log-likelihood.